5.1 계산 그래프 ~ 5.2 연쇄법칙

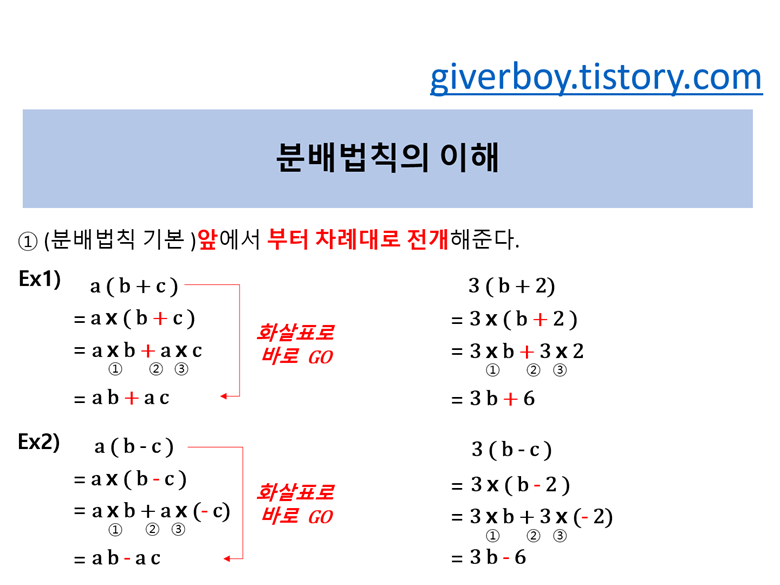
* 본 포스트는 책 바닥에서 시작하는 딥러닝(한빛미디어)을 바탕으로 작성되었습니다.* * * 참고사이트https://github.com/WegraLee/deep-learning-from-scratch/tree/master/ch05

Wegra Lee/Deep-Learning-from-Scratch 하작는닝 한러』디 (2017年)。 GitHub.github.com 위에 계정을 생성하여 WegraLee/스크래치에서 배우는 깊은 개발에 기여합니다.

계산 그래프 이번 장에서는 가중 파라미터의 기울기를 효율적으로 계산하는 오차 역전파법 back propagation에 대해 알아보겠습니다. 오차역전파법을 올바르게 이해하는 방법에는 수식에 의한 것과 계산 그래프에 의한 것 두 가지가 있습니다. 이번 장에서는 계산 그래프를 사용하여 오차 역전파법을 시각적으로 이해해 보려고 합니다. 계산 그래프 소개 계산 그래프는 계산 과정을 그래프로 나타낸 것입니다. 여러 노드와 에지*로 표현됩니다.*엣지:노드간 직선<계산그래프를 이용한 문제해결 흐름> 1.계산그래프 구성 2.그래프로 계산을 왼쪽에서 오른쪽으로 진행하고(순전파)그래프 예시문제를 풀어봅시다1.현빈 군은 슈퍼마켓에서 개당 100원짜리 사과 2개를 샀다. 이때 지불 금액을 구하시오. 단, 소비세가 10% 부과됩니다.

2. 현빈 군은 마트에서 사과 2개, 귤 3개를 샀다. 사과는 개당 100원, 귤은 개당 150원이다. 소비세가 10%대인 지불을 요구하시오.

계산 그래프의 이점 1. 국소적 계산 – 전체적으로 어떤 일이 일어나든 자신과 관련된 정보만으로 결과를 출력할 수 있다는 것. 아무리 복잡해도 각 노드에서는 단순화 계산에 집중하여 문제를 단순화할 수 있다.2. 중간 계산 결과를 모두 보관할 수 있다.3. 역전파를 통해 미분을 효과적으로 계산할 수 있다.- 순전파와 역전파를 활용하여 각 변수의 미분을 효율적으로 구할 수 있다!

연쇄법칙 chain rule 연쇄법칙 소개 연쇄법칙은 합성함수*의 미분에 대한 성질이다. *합성함수: 복수의 함수로 이루어진 함수 연쇄법칙의 원리는 《합성함수의 미분은 합성함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다》이다.예를 하나 보자.

위 식에서 x에 대한 z의 미분은 다음과 같이 쓸 수 있다.

연쇄 법칙과 계산 그래프

계산 그래프의 역전파

위의 역전파의 예는 y=f(x)라고 하는 계산의 역전파를 그려 본 것이다.역전파 계산 순서는 신호 E에 노드의 국소 미분(dy/dx)을 곱한 후 다음 노드로 전달하는 것!상기 z=t2 예에서 조사한 연쇄법칙 계산을 계산그래프로 보여주자.위의 역전파의 예는 y=f(x)라고 하는 계산의 역전파를 그려 본 것이다.역전파 계산 순서는 신호 E에 노드의 국소 미분(dy/dx)을 곱한 후 다음 노드로 전달하는 것!상기 z=t2 예에서 조사한 연쇄법칙 계산을 계산그래프로 보여주자.